Table of Contents
Abstract
This is a brief introduction to Cafun intended to help people understand Cafun's motivation and function. It outlines the basic properties of complex systems and why their tendency towards self-organization makes them worth studying. It introduces cellular automata as an ideal tool for simulating complex systems and sets Cafun in relation to their concept. Thereby, it tries to be accessible for both people with prior knowledge as well as absolute beginners.
Cafun is a modeling tool for complex systems. Before we start to take a closer look at Cafun itself lets try to understand what they are and what makes them so special. It's not possible to give a full overview about that broad topic here so we want to concentrate on the aspects which are relevant to Cafun. Complex systems are found throughout our all parts of our life. We encounter them in form of social groups like companies and societies, living organisms like people, animals and plants or in form of natural processes like the development of crystals. Complexity theorists search for general laws of these systems to gain deeper insights in their development, their structure and their behavior. They want to enable us to give better predictions in economics, biology, physics and other areas where complexity plays a role. Let's start our short excursion into the world of complex systems by defining some principles they have in common:
- Composition
-
Complex systems consist of many elements with individual properties and behavior. Examples: Social groups are composed of many people with individual interests and opinions. Living organisms are composed of many cells with an individual chemical composition. Crystals are composed of many molecules with an individual chemical structure.
- Decentralization
-
The elements' properties and behavior are the result of their local environment and individual history. It means that they are determined by a limited and local available amount of information. There is no omniscient central instance which controls them. Examples: The interests and opinions of people are determined by the ones of others just like their personal past and experiences. The chemical composition of cells is determined by their neighbor cells just like their past production of molecules. The chemical structure of molecules is determined by their chemical milieu and their development.
- Parallelism
-
Interactions between elements happen simultaneously. There is no prearranged sequence in which they take place. Examples: People exchange opinions at the same time. Cells influence and communicate with each other coevally. Molecules react with each other concurrently.
These conditions give rise to a web tied by the dependencies between the elements. Many people would argue that such a network must lead to chaos because experience tells us that we have to invest work and exercise control to achieve order. Though the examples presented above exhibit it all. It's an “order for free” as Stuart Kauffman calls it in his wonderful book “At Home In The Universe”. The key to this contradiction is self-organization. Under the influence of self-organization many individual elements emerge to a new abstract unit with its own properties and behavior. Just like people say: “The whole is more than the sum of its parts”. This unit can further be the element in another complex system with the same principles applied as before. Examples: Companies are elements of the market. People and animals are elements of social groups. Crystals are elements of cells. The questions that remain are: “Why do systems organize themselves?”, “What does it need for self-organization to occur?” and “What are the results?”. With Cafun you can find out for yourself. Experiment with different conditions and watch self-organization happen in real time! Complexity is neither total order nor chaos. It's something in between and that's what makes it so interesting.
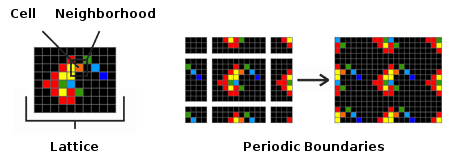
Cafun is an acronym for “Cellular Automata Fun”. As the name reveals, Cafun picks up the idea of cellular automata to perform its simulations. In the last decades many scientists realized that it needs more than the classic reductionism of mathematics to investigate complex systems. Cellular automata were proven as great tools for such applications and are now used throughout many disciplines of science especially by those doing research in complexity theory, artificial life and evolution. Although there are a lot of different kinds of cellular automata most of them are based on the following concept. The simulation takes place on a two dimensional lattice of so called “cells” where every single cell is surrounded by a neighborhood of eight more cells. Each of them is in a certain state which is represented by its color. The laws of a cellular automaton are summarized in a table of rules. These rules take the current state of a cell and the states of its neighbors into account to decide whether and how it will change. In one simulation step the rule table is applied to all cells on the lattice to determine their states in the next step. In order for every cell to have eight neighbors the lattice is characterized by so called periodic boundaries which are obtained by extending each side of it with the outermost cells of the other side. Cellular automata provide an excellent framework for the simulation of complex systems because they correspond to all of their principles that we have identified before - composition, decentralization and parallelism. The elements are represented by the cells of a cellular automaton. The roles of the local environment and individual history are taken by the neighborhood of each cell and its respective state. And finally, the condition of parallelism is fulfilled by the simultaneous application of rules.
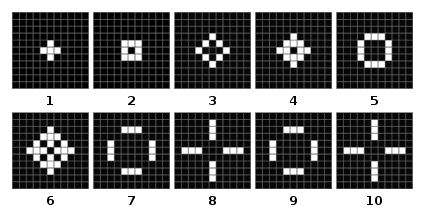
We can demonstrate the simulation of cellular automata with a simple example - the “Conway's Game of Life”. The cells of this famous cellular automaton can be in two states - “Dead” or “Alive” - and are governed by the following rules: A dead cell becomes alive when there are exactly three living cells in its neighborhood. A living cell dies if there are less than two or more than three cells in its neighborhood which are alive. Let's do a short simulation with dead cells painted black and living cells painted white. We start with a cross of five living cells. In the course of step two till six this simple pattern emerges into more complex ones until it gets stuck in something what complexity theorists call an "oscillator". As you can see it starts toggling between step seven and eight. No matter how long you simulate the system is trapped in a circle of order. However this is not the only direction Conway's Game of Life can take. Depending on the initial configuration of dead and living cells it can develop into many different patterns. Some who quickly die out, some who settle down to oscillators like the one before and others who give rise to an impressive complexity of new structures.
Cafun adopts the concept of the cellular automata described above but introduces a wealth of new ideas. Thereby it uses a slightly different nomenclature to ease the understanding of coherencies. The expression “universe” was substituted for “lattice” because it represents the whole virtual world in which the simulation takes place and the notion of “rule” was changed to “mutation” because it accounts for the switching to different cell type.
Cafun follows an object oriented approach to describe the laws of a cellular automaton. Instead of referring to a table of rules Cafun summarizes them in a set of cell types which have individual mutations assigned. Each cell in a universe of Cafun is considered to be an instance of such a cell type. Furthermore, Cafun allows cell types to be abstract. Abstract cell types cannot be instantiated by cells, but they can be implemented by actual cell types, which makes them inherit all of their mutations. This enables the summarization of common mutations of different cell types into one abstract cell type. Besides, it makes cells polymorphic since they behave as an instance of their actual cell type just as well as instances of the abstract cell types it implements. This kind of polymorphism is especially useful when defining conditions of mutations since it enables them to refer to abstract traits shared by cells of different cell types.
In every simulation step Cafun tries to apply a mutation to any cell in the universe, which will make it become an instance of a different cell type. Cafun allows only those mutations to be applied to a cell which belong to its own cell type or to the abstract ones its cell type implements. Just like in classic cellular automata, the application of a mutation in Cafun depends on the neighborhood of a cell, i. e. its eight neighbor cells. Therefore a mutation can have several conditions assigned, each specifying a requirement the neighborhood has to match for the mutation to be applied. For example, a condition can claim that there has to be a certain minimum or maximum number of cells in the neighborhood that share a certain cell type or that these cells are at special relative positions. In addition of being dependent on the neighborhood of a cell the application of Cafun's mutations is subjected to certain probabilities. If, for example, a mutation has a probability of 0.5 then it is applied in only half of the times when a cell neighborhood complies to its conditions. The consideration of probabilities was introduced to recreate the apparent indetermination of the real world. This leads to more realistic simulations and interesting new results. Since the neighborhood of a cell can comply to the conditions of several mutations they may find themselves in competition to each other. To prevent such a case, mutations have priorities assigned. If, however, several mutation share one priority, Cafun leaves it to changes what mutation to apply.
Cafun's new way of describing a cellular automaton makes it very convenient to model a complex system no matter whether it is a recreation of reality or an artificial one. All you have to do is to identify the basic elements of the system you're investigating and emulate them through cell types with individual mutations. Although Cafun's approach differs considerably from the one of classic cellular automata it remains compatible to most of them, especially those which correspond to the concept that was explained before. You can translate an existing cellular automaton into Cafun by creating a cell type for every state that is referred to by its rule table and assigning the respective mutations to it.
Cafun splits cellular automata into two parts, the simulation file and the universe. The simulation file takes over the task of describing the laws of the cellular automaton while the universe represents its current condition, i.e. the current type of all cells. During the simulation, the universe changes under the influence of the simulation file. Hence you always need to have both a simulation file and a universe to perform a simulation. Cafun's simulation files conform with the Extensible Markup Language, or XML for short. XML is an industry standard format with the advantages that it is readable by humans and that it can be easily transformed into other formats. Cafun's universes are stored as ordinary bitmap files and created in a similar manner like pictures in an image editing software. You can paint cells freehand, draw them in a line or fill entire areas of the universe with instances of one cell type. That is possible because in Cafun each cell type has a unique color assigned to it. So a universe can be unambiguously recreated from a bitmap file by translating the color of every single pixel into the type of a cell. However for your first simulations you might want to use the sample simulation files and universes that are distributed with Cafun.
In order to make simulations visually more appealing, Cafun offers means to beautify the view of a universe. Although this does not have any direct impact on the simulation it'll certainly help your simulations to attract attention. For this purpose Cafun's simulation can have a “make-up” view assigned, which can be activated interactively during simulation. A make-up view does nothing more than repainting the cells of the universe in a different color and applying a filter, like those used by image editing softwares. See for yourself about the effect!
Biologists describe an organism on many different levels of order. They divide it into organs with different functions, cells with different types, and so on until they end up with a huge number of different proteins. Most people think it is the genome which contains the information to all of these diverse stages. But unlike a blueprint of machine which can be implemented top-down and unambiguously, the information contained in a genome is processed bottom-up through all the different levels just enumerated until its final implementation is reached. Every single level is subject to mutual interaction and its environmental context. Organs, for example, communicate via hormones. Cells create a chemical milieu which alters the behavior of other cells and proteins take part in complex reactions which themselves are influenced by environmental factors like temperature. This sounds like a perfect example of complex systems under the influence self-organization. The genome though seems to play an important role by directing the development in special ways since organisms with similar genomes tend to exhibit similar traits. In some ways a simulation file in Cafun plays the same role as a genome in an organism. Unlike their biological counterparts which express their information in form of chains of amino acids Cafun's simulation files directly define a set of cell types with individual properties and rules. However both follow the same intention which is to give rise to and guide the course of a complex system.